Dr. Carlo Pescio La Rappresentazione Grafica dei Modelli

Pubblicato su Computer Programming No. 43

Rappresentazioni grafiche
Sin dalla seconda puntata di questa serie, abbiamo visto come sia possibile rappresentare un modello object oriented di un sistema, ancora privo di relazioni tra le classi, tramite una semplice tabella; tuttavia, con l'introduzione delle relazioni la tabella diviene presto limitativa ed e' invece consigliabile l'uso di rappresentazioni grafiche. In questa puntata verranno introdotti e discussi due formalismi di tipo grafico per la rappresentazione dei modelli object oriented, seguendo due tra le piu' complete e diffuse metodologie per l'analisi dei sistemi, ovvero Coad/Yourdon e Booch. Porre l'accento su due diversi modelli, anziche' concentrarsi unicamente su uno di essi, ci consentira' di osservare e discutere alcune differenze metodologiche nei due approcci.

In effetti, avevo inizialmente pianificato di introdurre anche alcuni elementi da un terzo approccio all'object oriented analysis, ovvero OMT (Object Modeling Technique). Tuttavia, recentemente il suo ideatore James Rumbaugh e' passato alla Rational di Booch, ed e' opinione generale che OMT, peraltro abbastanza diffusa in alcuni paesi europei ma non molto in USA, verra' ben presto "fusa" con il metodo di Booch; per tale ragione, non discuteremo OMT nell'ambito dell'analisi object oriented, e ci limitermo a riprenderne alcune interessanti idee molto generali piu' avanti, quando arriveremo a parlare di design.

Sempre in questa puntata, introdurremo un elemento essenziale per le rappresentazioni di sistemi complessi, il cosiddetto livello dei soggetti (o delle categorie di classi, a seconda dell'autore), motivandone l'importanza in base a studi sulla memoria a breve e lungo termine degli esseri umani.

Considerazioni psicologiche
Ogni autore di testi su OOA/OOD, nonche' ogni ideatore di un nuovo approccio all'analisi o al design, sente spesso l'esigenza di introdurre un diverso formalismo grafico. Se da una parte cio' e' abbastanza comprensibile, l'effetto ottenuto e' invece indesiderabile, in quanto chi si avvicina ad un nuovo metodo deve necessariamente apprendere un nuovo "linguaggio" grafico.

Il vero problema non riside tuttavia nella varieta' dei formalismi grafici, ma nella relativa immaturita' degli stessi; esistono infatti due importanti criteri per valutare la bonta' di una rappresentazione grafica: osservanza di alcuni canoni prettamente tecnici, e rispetto di criteri psicologici piu' ampi. Quando si sale nel livello di astrazione (e le rappresentazioni grafiche a livello di OOA sono molto astratte), il lato tecnico passa in secondo piano, mentre grande rilevanza assumono gli aspetti psicologici.

E' infatti provato da numerosi esperimenti come la rappresentazione dell'informazione influisca profondamente sulla comprensione dell'informazione stessa. Le specifiche dei sistemi, siano esse realizzate con metodi grafici o con linguaggi descrittivi, non fanno eccezione; per richiamare un esempio forse piu' familiare al lettore, basti pensare quanto un diverso stile di indentazione del codice influisca sulla nostra capacita' di comprendere rapidamente (e correttamente) il flusso del codice stesso. Si veda [1] per una attenta analisi del fenomeno.

Sempre considerazioni di tipo psicologico stanno alla base di alcune delle "norme di buona progettazione" che ho elencato in una precedente puntata, estrapolate in gran parte dalla mia personale esperienza. Ad esempio, ricorderete che una delle regole recitava: "Le classi dovrebbero essere limitate ad uno stesso livello di astrazione..."; piu' recentemente ho scoperto in [2] che diversi esperimenti confermano come il passaggio da una dimensione fisica ad un'altra richieda un "riaggiustamento" mentale, caratterizzato da un rallentamento nella nostra velocita' di elaborazione delle informazioni.

Tornando alle rappresentazioni grafiche, purtroppo ben poche hanno solide basi psicologiche; l'unico riferimento esplicitio che ho trovato e' stato in Coad/Yourdon, e verra' ripreso piu' avanti in questo articolo. Simili considerazioni si potrebbero estendere a gran parte dei Visual Languages molto di moda, ma si uscirebbe dallo scopo della rubrica; in ogni caso, tenete sempre presente che, mentre su piccoli progetti il problema di una appropriata rappresentazione dell'informazione puo' essere marginale, in grandi progetti, dove la quantita' di informazione da trasmettere e' decisamente piu' consistente, non basta affidarsi all'estetica ed al buon senso, ma occorrono dei criteri solidi, oggettivi e sperimentati.

Classi e Oggetti
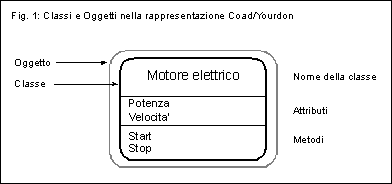
In figura 1 possiamo vedere la rappresentazione Coad/Yourdon per una classe e per un oggetto della classe: il rettangolo nero interno rappresenta la classe, che viene definita dal nome, dai suoi attributi e dai metodi che rende disponibili; il rettangolo grigio esterno rappresenta un oggetto instanza della classe. A livello di analisi, gli oggetti non sono in se' molto interessanti (il passo di maggiore importanza e' modellare le classi e le relazioni tra classi), tuttavia e' importante avere una rappresentazione anche per i singoli oggetti di una classe, sia per la loro utilita' nel modellare gli use case (li vedremo nella prossima puntata), sia per uniformita' con il successivo livello di design, dove effettivamente saremo interessati anche al singolo oggetto.

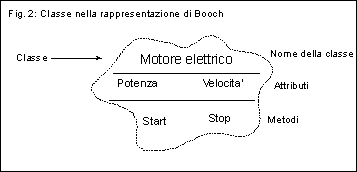
Booch utilizza invece due rappresentazioni distinte per la classe e per l'oggetto (figura 2 e figura 3): l'uso di un contorno tratteggiato per il simbolo di "classe" sottintende l'idea, piuttosto approssimata ma comunque abbastanza calzante, che la classe sia un concetto piu' astratto, mentre l'oggetto, caratterizzato da un contorno pieno, e' considerato un elemento piu' concreto nel modello.

Come vedremo tra breve, l'idea di Coad/Yourdon di fondere in un unico simbolo classe ed oggetti ha un suo valore a livello di rappresentazione simbolica, in quanto consente di esprimere al meglio alcune particolarita' delle relazioni tra classi, dettagli che non vengono posti in evidenza dalla rappresentazione di Booch. Si tratta comunque piu' di una raffinatezza che di una vera e propria differenza nel contenuto informativo delle due rappresentazioni.

Generalizzazione/Specializzazione
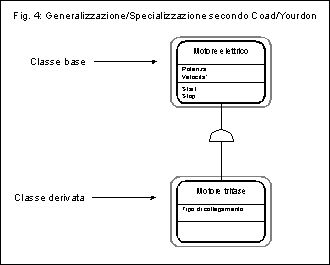
In figura 4 e figura 5 possiamo vedere le rappresentazioni secondo Coad/Yourdon e Booch della relazione di generalizzazione/specializzazione. Come vedete sono molto simili, ed entrambe rispettano un criterio tecnico fondamentale, ovvero sono rappresentazioni orientate (sia l'arco di circonferenza che la freccia hanno un verso univoco). Cio' consente di disporre le classi in una qualunque posizione relativa senza ambiguita' nella rappresentazione, per quanto sia preferibile, quando possibile, porre le classi base in alto e le classi derivate in basso.

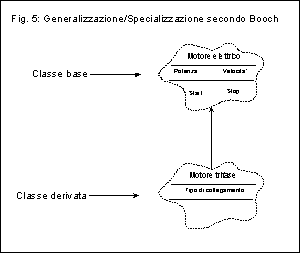
Quando piu' classi sono derivate dalla stessa classe base, nel metodo Coad/Yourdon esse possono condividere il simbolo di derivazione (nel quale quindi entrano piu' linee), mentre secondo Booch ogni classe ha una sua freccia di derivazione. Va detto che l'uso appropriato del metodo di Coad/Yourdon e' molto piu' flessibile ed espressivo, in quanto consente il clustering di alcune classi derivate che, per qualche ragione, siano concettualmente piu' vicine tra loro: in questo caso, esse condivideranno lo stesso simbolo di derivazione.

Notiamo infine che in figura 4 la derivazione e' rappresentata come una connessione tra due classi (i rettangoli neri interni) e non tra oggetti (i rettangoli grigi esterni), in accordo all'idea intuitiva di specializzazione di una classe (non di un oggetto) in un'altra.

Strutture Tutto/Parti
In figura 6 e 7 possiamo vedere le rappresentazioni delle strutture tutto/parti secondo Coad/Yourdon e Booch: notiamo che nuovamente la rappresentazione e' orientata in entrambi i casi. Nelle strutture tutto/parti, come si vede in figura 6, il simbolo caratterizzante (il triangolino) non viene condiviso: la ragione sta nel fatto che non sarebbe altrimenti possibile associare la giusta cardinalita' alla relazione. Nell'esempio dato, la cardinalita' e' molto semplice: un motore elettrico ha esattamente un rotore ed uno statore, ed ogni rotore (o statore) e' parte di uno ed un solo motore elettrico.

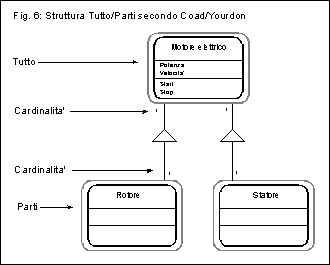
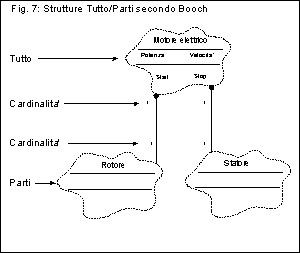
Nota importante: il modello Coad/Yourdon associa la cardinalita' alla classe piu' vicina (come nel modello entita'/relazione), mentre Booch la assegna alla classe opposta. Ovvero, in figura 6 la cardinalita' "1" vicino a "Rotore" indica che il Rotore appartiene ad uno ed un solo Motore, e la cardinalita' "1" vicino a Motore indica che Motore e' composto da 1 ed un solo Rotore. Secondo Booch il significato e' quello opposto (ed a parer mio molto meno chiaro); vedremo un ulteriore esempio tra breve.

Notiamo infine che nella rappresentazione Coad/Yourdon la struttura tutto/parti e' rappresentata come un collegamento tra oggetti (rettangoli esterni grigi) e non tra le classi. Dal mio punto di vista, questa e' una raffinatezza del modello di Coad/Yourdon non presente in Booch o in altri modelli: si formalizza infatti in tal modo che "Ogni oggetto della classe Motore e' composto da un oggetto della classe Statore e da un oggetto della classe Rotore". Connettere direttamente le classi, anziche' gli oggetti, corrisponderebbe in effetti a dire che "La classe dei Motori ha come parti le classi dei Rotori e degli Statori", asserzione di per se' quantomeno imprecisa se non errata. Questo non intacca in modo sensibile la chiarezza della rappresentazione secondo Booch, poiche' chi legge e' in grado di interpretare correttamente la specifica in ogni caso, ma va comunque apprezzata l'attenzione ai dettagli in Coad/Yourdon.

Relazioni Generiche
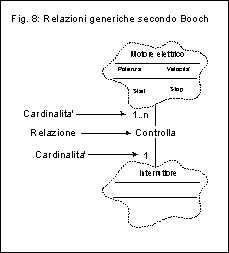
Come abbiamo visto nella puntata precedente, nel modello di Booch esiste il concetto di "relazione", in tutto e per tutto simile a quella del modello entita'/relazione, concetto invece assente in altri modelli come Coad/Yourdon. In figura 8 abbiamo un esempio di relazione generica, da leggersi come "Un interruttore controlla uno o piu' motori, un motore e' controllato da uno ed un solo interruttore". Prestate attenzione al fatto che, come gia' ribadito in precedenza, la lettura delle cardinalita' e' rovesciata rispetto al modello entita'/relazione o all'uso nel Coad/Yourdon relativamente alle strutture tutto/parti. Notiamo inoltre che la "relazione generica" non e' orientata (cosi' come non lo e' nel modello entita' relazione), anche se cio' genera non pochi problemi nella scelta di un nome appropriato per la relazione stessa: ad esempio, in figura 8 il nome "Controlla" per la relazione ha senso se la leggiamo "dal basso verso l'alto", ma non viceversa; queste imprecisioni sono abbastanza comuni nel modello entita'/relazioni, tuttavia non e' stata forse la scelta piu' saggia propagarle nel modello di Booch.

Revoche ed Eccezioni
Molti fanno risalire le origine della programmazione object oriented al Simula 67 ed agli studi sulla simulazione dei sistemi. D'altro canto, l'analisi ed il design object oriented sono state in gran parte una ricaduta di vecchi studi sull'intelligenza artificiale, in maggior misura di quelli sulle reti semantiche: basti vedere come le discussioni in [3] e [4] siano di estremo interesse per chi oggi si occupa di object oriented technology.

Uno dei classici problemi nelle reti semantiche e' quello delle eccezioni e delle revoche: l'esempio classico e' quello della gerarchia di classificazione animale/animale che vola/uccello/struzzo; notiamo che lo struzzo non vola, e quindi una gerarchia che sembrava sensata concentrandosi solo sulle relazioni dirette diventa non valida a causa di una eccezione transitiva. Gli studi sulle reti semantiche hanno approfondito l'argomento, senza tuttavia ottenere vere e proprie soluzioni eleganti, complete, e computazionalmente efficienti. Nel campo object oriented, si e' piu' o meno deliberatamente ignorato il problema, ed infatti non esiste un meccanismo standard per definire l'eccezione, e quindi non abbiamo una corrispondente rappresentazione (attenzione a non confondere l'eccezione in una gerarchia di ereditarieta' con le eccezioni a run-time gestite ad esempio dal C++). Sta al progettista ristrutturare la gerarchia in modo che abbia senso, anche a costo di duplicare l'informazione: ad esempio, eliminando la classe "animale che vola" dalla gerarchia; questo da un lato ci priverebbe di una classe astratta cui pipistrelli, insetti, uccelli, eccetera appartengono, ma dall'altro ci restituirebbe la correttezza semantica che mancava al primo modello.

Il magico numero sette
E' importante ricordare continuamente che il risultato dell'analisi ed del design e' un prodotto che verra' letto, studiato, modificato da esseri umani; cio' e' vero anche per il risultato della codifica (anche se alcuni programmatori scrivono codice leggibile solo da una macchina!), ma e' a maggior ragione evidente per le fasi piu' astratte di progettazione.

Consideriamo ora un sistema di media complessita', con una cinquantina di classi e diverse decine di relazioni: esso risultera' difficilmente comprensibile nella sua interezza, non perche' sia intrinsecamente complesso, ma in quanto la sua struttura tende a saturare le capacita' organizzative della mente e soprattutto della memoria umana.

In un saggio di grandissima importanza, Miller [5] ha dimostrato come gli esseri umani siano in grado di comprendere e ricordare al meglio diagrammi composti da un numero di entita' variabili tra il 5 ed il 9 (da cui, il magico numero sette piu' o meno due). Questo e' stato uno dei principi guida di alcuni metodi, basati sui raffinamenti successivi, come i diagrammi a bolle. In effetti, in uno studio successivo [6] lo stesso autore ha osservato che il fattore piu' limitante non e' costituito dal numero di oggetti, ma dal numero di gruppi di oggetti; in particolare, il "nuovo" limite della memoria cosi' identificato e' stato di tre gruppi ognuno composto al piu' di tre oggetti.

Come sempre, e' possibile interpretare ed utilizzare simili risultati sperimentali in modi diversi; il rispetto piuttosto letterale della regola, costringerebbe ad avere una gerarchia diagrammi molto semplici, sempre piu' raffinati e dettagliati. In tal caso, tuttavia, sarebbe difficile ottenere una comprensione del dominio che sia allo stesso tempo ampia (ovvero abbracci l'intero sistema) e profonda (ovvero arrivi ovunque al livello di dettaglio). Va detto comunque che solo i migliori progettisti sono capaci di simili "visioni" del sistema, e che anzi una delle caratteristiche determinanti per un buon progettista e' proprio di riuscire ad avere e a mantenere tali visioni.

Una interpretazione meno radicale dei risultati di Miller e' che l'attenzione umana va guidata, riunendo oggetti e classi vicine (da un punto di vista semantico) in gruppi che facilitino la comprensione del singolo cluster di classi ed il passaggio da un cluster all'altro.

Una seconda, importante interpretazione di quanto sopra e' che un buon tool (ad es. uno strumento CASE) dovrebbe consentire di vedere solo l'informazione desiderata: le sole classi, le classi e le relazioni, i dettagli di una singola classe, e cosi' via. Su questo ritorneremo in una puntata futura.

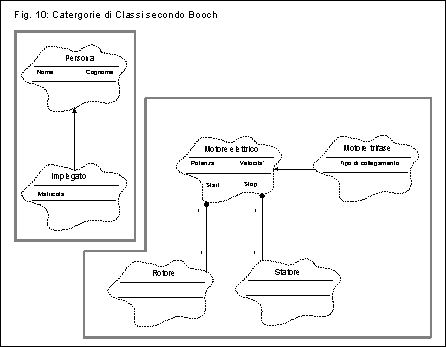
Sia il metodo di Coad/Yourdon che il metodo di Booch forniscono un modello di clustering concettuale per le classi, che in Coad/Yourdon e' chiamato Spazio dei Soggetti e in Booch e' definito come Categorie di Classi. In figura 9 e 10 e' rappresentato un semplice esempio, nei due diversi approcci: supponiamo di dover modellare una centrale, nella quale alcuni operai devono supervisionare il funzionamento di alcuni motori elettrici. Nel nostro modello figureranno Persone, Operai, Motori, Rotori e Statori, tuttavia anche in una rappresentazione cosi' semplice possiamo evidenziare due cluster ben distinti, uno incentrato sulle persone ed uno sui motori; notiamo che i cluster nell'esempio dato sono autocontenuti, ma in generale potremo avere relazioni tra classi appartenenti a cluster diversi. Difficilmente, se abbiamo fatto un buon lavoro, tali relazioni saranno di tipo generalizzazione/specializzazione, che rappresenta di fatto un legame semantico molto forte, rispetto ad esempio al tutto/parti.

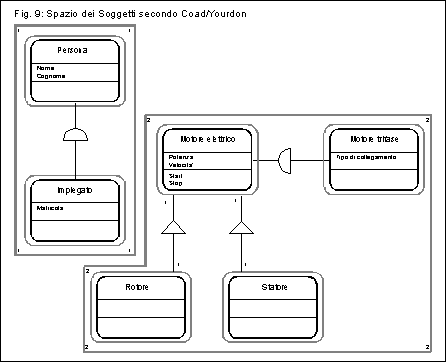
Osserviamo che nel modello di Coad/Yourdon viene riportato un numero ad ogni angolo; tale numero viene poi associato in un dizionario dei dati al nome del soggetto. Nulla impedisce di scrivere per esteso il nome del soggetto stesso, tranne che la leggibilita' del tutto lascerebbe forse a desiderare. Inutile dire che un buon tool di CASE diventa rapidamente utile, se non necessario, per tenere traccia di tutte le associazioni; detto tool dovrebbe poi essere in grado, come abbiamo visto, di fornirci una vista d'insieme di un soggetto (con il solo nome) o di esploderne la struttura, e cosi' via.

Il modello di Booch non pone grande accento sui soggetti, o meglio sulle categorie di classi. Esse sono tuttavia del tutto equivalenti ai soggetti di Coad/Yourdon, e la successiva discussione potra' essere applicata indipendentemente dal modello scelto. Ricordiamo comunque che l'uso dei soggetti e' opzionale, e che se il dominio del problema e' piccolo non si avra' di norma la necessita' di definirli ed utilizzarli.

Identificare i Soggetti
Questo e' un vero e proprio passo di "analisi nell'analisi"; un Soggetto rappresenta, ad un piu' elevato livello di astrazione, un insieme di classi, la cui distanza concettuale, o semantica, sia in qualche misura minore della norma (vedere nuovamente l'esempio delle figure 9 e 10). Esistono tuttavia anche in questo caso delle linee guida, per identificare i soggetti in un diagramma esistente (approccio bottom-up): la classe di piu' alto livello in una gerarchia di generalizzazione/specializzazione diventa un soggetto (questo include le classi isolate), che congloba tutta la gerarchia. A questo punto si considerano i vari soggetti e si verifica che siano autonomi, autocontenuti: le connessioni dovute a strutture del tipo tutto/parti, a relazioni generalizzate, o a dipendenze di utilizzo devono essere nulle o minime. Se cio' non avviene, i soggetti con un alto indice di accoppiamento sono degli ottimi candidati alla fusione in un unico soggetto. Finita questa fase, possiamo passare ad una seconda analisi top-down, per esplorare i confini del dominio del problema (notiamo la somiglianza con altri passi di analisi); a questo punto, dovremo validarne l'importanza, con una checklist del tipo: esistono dei soggetti che la nostra conoscenza del problema ci suggerisce vadano aggiunti? Sono in qualche modo presenti ma partizionati tra alcuni dei soggetti esistenti? Hanno realmente senso ai fini del problema?

Naturalmente, e' possibile applicare un approccio top-down sin dall'inizio, definendo il dominio in base ai soggetti ed in seguito identificando le classi all'interno di ogni cluster; alcuni autori suggeriscono questo approccio per i grandi sistemi. Tuttavia, molte persone faticano ad affrontare sin dall'inizio un metodo troppo astratto, e per tale ragione e' spesso consigliabile un approccio misto, in parte bottom-up ed in parte top-down.

E' un buon modello?
A questo punto abbiamo ottenuto un modello abbastanza raffinato del dominio del problema, e lo abbiamo rappresentato graficamente in modo da poterlo discutere e comprendere piu' agevolmente. Resta comunque un grande interrogativo: e' un buon modello? Ovvero, e' un modello completo e corretto del sistema, ed ha una buona qualita'? Affronteremo tali interrogativi nella prossima puntata.

Reader's Map

Molti visitatori che hanno letto questo articolo hanno letto anche:

Bibliografia
[1] Shepard, Kruesi: "The Effects of Symbology and Spacial Arrangement on Software Specification in a Coding Task", Proc. Trends and Applications 1981: Advances in Software Technology, IEEE.

[2] Kosslyn, Shwartz: "Empirical Constraints on Theories of Visual Mental Imagery", Attention and Performance vol. IX, Erlbaum, 1981.

[3] W. A. Woods: "What's in a Link: Foundations for Semantic Networks", ristampato in "Readings in Knowledge Representation", Morgan Kaufmann Publishers Inc., 1985.

[4] R. J. Brachman: "What IS-A Is and Isn't: An Analysis of Taxonomic Links in Semantic Networks", IEEE Computer, 1983.

[5] G. A. Miller: "The Magical Number Seven, Plus or Minus Two: Some Limits on our Capacity for Processing Information", The Psychological Review 63, N. 2, 1956.

[6] G. A. Miller: "The Magic Number Seven After Fifteen Years", Studies in Long Term Memories, John Wiley & Sons, 1975.

Biografia
Carlo Pescio svolge attività di consulenza in ambito internazionale sulle metodologie di sviluppo Object Oriented e di programmazione in ambiente Windows. È laureato in Scienze dell'Informazione, membro dell'Institute of Electrical and Electronics Engineers Computer Society, dei Comitati Tecnici IEEE su Linguaggi Formali, Software Engineering e Medicina Computazionale, dell'ACM e dell'Academy of Sciences di New York. Può essere contattato tramite la redazione o su Internet come pescio@programmers.net